A fake Facebook event disguised as a math problem has been one of its top posts for 6 months
-
People try and use commas for this sort of clarification and are eviscerate for it.
With these sort of math problems, the rules are taught early and then all subsequent math is written in an unambiguous form.
Language has the oddity of going the other way around where the rules get more complex as a display for advanced skills.
eviscerated
God, can you even spell???
Get your act together./s
-
Anyone on Facebook that attempts to answer this or engage within its comments has already failed the test.
Anyone on Facebook
that attempts to answer this or engage within its commentshas already failed the test. -
For me it's the arguments when there is a parentheses but no operator (otherwise known as implied multiplication) in these baits e.g. 15 + 2(4 - 2)
If you don't know operator orders I have given up long ago, but I have seen a few lengthy discussions about this
Oh yeah, that's a fun one.
Where I live, this would be considered juxtaposition, at least by uni professors and scientific community, so 2(4-2) isn't the same as 2×(4-2), even though on their own they're equal.
This way, equations such as 15/2(4-2) end up with a definite solution.
So,
15/2(4-2) = 3.75
While
15/2×(4-2) = 15
Usually, however, it is obvious even without assuming juxtaposition because you can look at previous operations. Not to mention that it's most common with variables (Eg. "2x/3y").
-
I'm more worried about the gratuitous comma and what it means for the state of education.
What, gratuitous, comma?
-
I'm sure we're all geniuses here, but just in case...
Please excuse my dear aunt Sally.
Parenthesis, exponents, multiplication, division, addition, subtraction.
Why? Because a bunch of dead Greeks say so!
3x3-3÷3+3
(3x3)-(3÷3)+3
9-1+3
8+3
11
The "why" goes a little further than that.
In actuality, it's because of fundamental properties of operations
- Commutation
a + b = b + a
a×b = b×a
- Association
(a + b) + c = a + (b + c)
(a×b)×c = a×(b×c)
- Identity
a + 0 = a
a×1 = a
If you know that, then PEMDAS and such are useless because they're derived from those properties but do not fully encompass them.
Eg.
3×2×(2+2) = 3×(4+4) = 12+12 = 24
This is a correct solution that is improper if you're strictly adhering to PEMDAS rule as I've done multiplication before parenthesis from right to left.
I could even go completely out of order by doing 3×2×(2+2) = 2×(6+6) and it will still be correct
-
This post did not contain any content.
Arguing about maths is like dancing to architecture.
-
I hate most math eduction because it's all about memorizing formulas and rules, and then memorizing exceptions. The user above's system is easier to learn, because there's no exceptions or weirdness. You just learn the rule that division is multiplication and subtraction is addition. They're just written in a different notation. It's simpler, not more difficult. It just requires being educated on it. Yes, it's harder if you weren't obviously, as is everything you weren't educated on.
That's because (strictly speaking) they aren't teaching math. They're teaching "tricks" to solve equations easier, which can lead to more confusion.
Like the PEMDAS thing that's being discussed here. There's no such thing as "order of operations" in math, but it's easier to teach by assuming that there is.
Edit:
To the people downvoting: I want to hear your opinions. Do you think I'm wrong? If so, why? -
You understand that gen x starts around 1965, right? Your stat says they're mostly getting fucked too.
And you understand that 68 is after 65? They're not getting. Fucked, they're the last ones to be able to afford housing ownership. If the average is 68 that means one side of the bell curve extends well into the generation.
-
You understand that gen x starts around 1965, right? Your stat says they're mostly getting fucked too.
I'm on the cusp of X and millennial, so I've been around plenty of both.
Some X's have done well for themselves, but those without a bit of luck and assistance have mostly had to give up on big dreams of housing security and family.
Millennials have had it tougher, but many of them still got there, with a bit more luck and assistance.
It's been a long decline, with the concentration of capital making it harder for most of us every year. The generational divide is just another distraction from class warfare.
-
So order of operations is hard?
The issue normally with these "trick" questions is the ambiguous nature of that division sign (not so much a problem here) or people not knowing to just go left to right when all operators are of the same priority. A common mistake is to think division is prioritised above multiplication, when it actually has the same priority. Someone should have included some parenthesis in PEDMAS aka. PE(DM)(AS)

-
The issue normally with these "trick" questions is the ambiguous nature of that division sign (not so much a problem here) or people not knowing to just go left to right when all operators are of the same priority. A common mistake is to think division is prioritised above multiplication, when it actually has the same priority. Someone should have included some parenthesis in PEDMAS aka. PE(DM)(AS)

The same priority operations can be done in any order without affecting the result, that's why they can be same priority and don't need an explicit order.
6 × 4 ÷ 2 × 3 ÷ 9 evaluates the same regardless of order. Can you provide a counter example?
-
What, gratuitous, comma?
The one after the prove.
-
Arguing about maths is like dancing to architecture.
Hey, some architecture is asking for it like Stonehenge
-
The same priority operations can be done in any order without affecting the result, that's why they can be same priority and don't need an explicit order.
6 × 4 ÷ 2 × 3 ÷ 9 evaluates the same regardless of order. Can you provide a counter example?
Oh my god now this is going to be Lemmy’s top thread for 6 months, isn’t it?
Btw, yeah I’m with you on this, you just need to know the priorities and you’re good, because the order doesn’t matter for operations with the same priority
-
The same priority operations can be done in any order without affecting the result, that's why they can be same priority and don't need an explicit order.
6 × 4 ÷ 2 × 3 ÷ 9 evaluates the same regardless of order. Can you provide a counter example?
So let's try out some different prioritization systems.
Left to right:
(((6 * 4) / 2) * 3) / 9 ((24 / 2) * 3) / 9 (12 * 3) / 9 36 / 9 = 4Right to left:
6 * (4 / (2 * (3 / 9))) 6 * (4 / (2 * 0.333...)) 6 * (4 / 0.666...) 6 * 6 = 36Multiplication first:
(6 * 4) / (2 * 3) / 9 24 / 6 / 9Here the path divides again, we can do the left division or right division first.
Left first: (24 / 6) / 9 4 / 9 = 0.444... Right side first: 24 / (6 / 9) 24 / 0.666... = 36And finally division first:
6 * (4 / 2) * (3 / 9) 6 * 2 * 0.333... 12 * 0.333.. = 4It's ambiguous which one of these is correct. Hence the best method we have for "correct" is left to right.
-
Oh my god now this is going to be Lemmy’s top thread for 6 months, isn’t it?
Btw, yeah I’m with you on this, you just need to know the priorities and you’re good, because the order doesn’t matter for operations with the same priority
Except it does matter. I left some examples for another post with multiplication and division, I'll give you some addition and subtraction to see order matter with those operations as well.
Let's take:
1 + 2 - 3 + 4Addition first:
(1 + 2) - (3 + 4)
3 - 7 = -4Subtraction first:
1 + (2 - 3) + 4
1 + (-1) + 4 = 4Right to left:
1 + (2 - (3 + 4))
1 + (2 - 7)
1 + (-5) = -4Left to right:
((1 + 2) - 3) + 4
(3 - 3) + 4 = 4Edit:
You can argue that, for example, the addition first could be(1 + 2) + (-3 + 4)in which case it does end up as 4, but in my opinion that's another ambiguous case. -
This post did not contain any content.
Every one of these only makes me say "wouldn't it be great if we did everything with RPN"?
-
So let's try out some different prioritization systems.
Left to right:
(((6 * 4) / 2) * 3) / 9 ((24 / 2) * 3) / 9 (12 * 3) / 9 36 / 9 = 4Right to left:
6 * (4 / (2 * (3 / 9))) 6 * (4 / (2 * 0.333...)) 6 * (4 / 0.666...) 6 * 6 = 36Multiplication first:
(6 * 4) / (2 * 3) / 9 24 / 6 / 9Here the path divides again, we can do the left division or right division first.
Left first: (24 / 6) / 9 4 / 9 = 0.444... Right side first: 24 / (6 / 9) 24 / 0.666... = 36And finally division first:
6 * (4 / 2) * (3 / 9) 6 * 2 * 0.333... 12 * 0.333.. = 4It's ambiguous which one of these is correct. Hence the best method we have for "correct" is left to right.
It’s ambiguous which one of these is correct. Hence the best method we have for “correct” is left to right.
The solution accepted anywhere but in the US school system range from "Bloody use parenthesis, then" over "Why is there more than one division in this formula why didn't you re-arrange everything to be less confusing" to "50 Hertz, in base units, are 50s^-1^".
More practically speaking: Ultimately, you'll want to do algebra with these things. If you rely on "left to right" type of precedence rules re-arranging formulas becomes way harder because now you have to contend with that kind of implicit constraint. It makes everything harder for no reason whatsoever so no actual mathematician, or other people using maths in earnest, use that kind of notation.
-
So let's try out some different prioritization systems.
Left to right:
(((6 * 4) / 2) * 3) / 9 ((24 / 2) * 3) / 9 (12 * 3) / 9 36 / 9 = 4Right to left:
6 * (4 / (2 * (3 / 9))) 6 * (4 / (2 * 0.333...)) 6 * (4 / 0.666...) 6 * 6 = 36Multiplication first:
(6 * 4) / (2 * 3) / 9 24 / 6 / 9Here the path divides again, we can do the left division or right division first.
Left first: (24 / 6) / 9 4 / 9 = 0.444... Right side first: 24 / (6 / 9) 24 / 0.666... = 36And finally division first:
6 * (4 / 2) * (3 / 9) 6 * 2 * 0.333... 12 * 0.333.. = 4It's ambiguous which one of these is correct. Hence the best method we have for "correct" is left to right.
Maybe I'm wrong but the way I explain it is until the ambiguity is removed by adding in extra information to make it more specific then all those answers are correct.
"I saw her duck"
Until the author gives me clarity then that sentence has multiple meanings. With math, it doesn't click for people that the equation is incomplete. In an English sentence, ambiguity makes more sense and the common sense approach would be to clarify what the meaning is
-
I was good at math and it was one of my favorite core subjects in school, so I know I'm a weirdo but... I never understood how people couldn't understand basic PEMDAS/BEDMAS/Whatever-the-fuck-your-country-calls-it.
Obviously these problems are shitty engagement bait because they don't use parentheses, but still, seeing people fuck up the fact that Multiplication AND Division occur at the same time, and then the next step is Addition AND Subtraction just stupefies me.
Like, did you sleep through 4 years of elementary school to miss that fact??? Even in middle school pre-algebra teachers still did PEMDAS refreshers. I get that once I get out of college I'm probably gonna forget half the pre-calc shit I learned because I won't need it, and I'm not being drilled on it everyday like people in school are, but PEMDAS is a fundamental and basic daily life skill that everyone should know...
I really wish we gave a fuck about US education.
I never understood how people couldn’t understand basic PEMDAS/BEDMAS/Whatever-the-fuck-your-country-calls-it.
There's no "whatever-the-fuck-your-country-calls-it", the US is the only country using it, and only up to high school. At least I'm not seeing any papers coming out of the US relying on it so at some point they're dropping it and do what everyone else is doing: Write equations such that you don't need a left-to-right rule to disambiguate things. Also, using multiplication by juxtaposition (2x + 4x^2^).
-
-
-
UK Competition and Markets Authority (CMA) is Cracking Down on Google; Roadmap Include Requiring Choice Screen for Search Providers, Fair Ranking, Publisher Transparency, and Data Portability.
Technology 1
1
-
-
-
Is it feasible and scalable to combine self-replicating automata (after von Neumann) with federated learning and the social web?
Technology 1
1
-
[Open question] Why are so many open-source projects, particularly projects written in Rust, MIT licensed?
Technology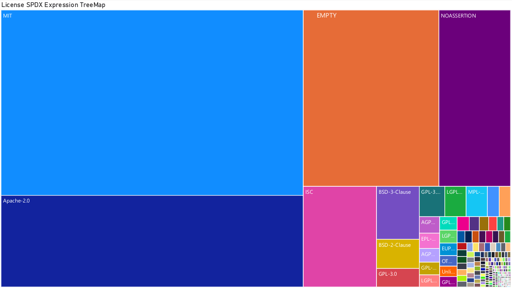 1
1
-





